Quantum information theory of Neural Collapse in Deep Learning Models

Advisor: Stefano Recanatesi

Contact Information: stefano@technion.ac.il

Abstract:

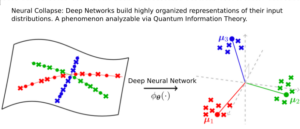
Deep Neural Network (DNNs) trained to classify images (e.g. object recognition) output a class (e.g. the object in the image) given a specific image from the distribution of inputs.

During training, these models develop features or representations for different classes that ‘collapse’ or converge within the same class while maintaining a certain distance from features of other classes. This behavior, is known as Neural Collapse, and is a key aspect of modern machine learning. This project focuses on the exploration of Neural Collapse, through the lens of quantum information theory. Quantum information theory allows to understand how input distributions (e.g. all the images containing an airplane) should be optimally encoded in the network’s representation, with respect to all other input distributions (cars, trucks…) so as to maximize the flow of information through the network.

Transmitting quantum states through a channel is essentially like transmitting probability densities across it, which is remarkably similar to a network, once analyzed through this lens. The project will employ covariance operators and Jensen-Shannon Divergence to describe the geometry of the representation space between classes. We will apply Holevo’s Theorem, a specific theorem in Quantum Information Theory, to establish upper bounds on the information that can be extracted from this space. This application will provide a novel perspective on the geometry of feature spaces in deep learning.

The ultimate goal of this project is to gain new insights that could help improve how we train these models, making them learn more effectively. By understanding the underlying mechanisms of Neural Collapse, we could potentially enhance the training process of deep learning models and improve their performance.