Below you can find some of the projects I’ve worked on as well as ongoing research.
Self-organization of turbulent flows
Turbulence is usually viewed as the breaking up of a large scale flow into ever smaller chaotic motions. A quantitative manifestation of this picture is the energy cascade, with energy flowing from large scales to increasingly smaller ones, where it is eventually dissipated by viscosity.
On the contrary, when most of the energy is concetrated in 2d modes, energy is transferred to progressively larger scales–in an inverse cascade. This process can then terminate in the self-organization of the turbulence into a large scale mean flow, a so-called condensate, on top of small scale fluctuations.
Although such 2d turbulence may seem like an abstract concept, many natural flows are effectively restricted to two dimensions: planetary-scale flows in the ocean and atmosphere are an example, and they are often made up of coherent currents or vortices in combination with chaotic fluctuations.
Our work is centered around the following questions: What are the rules of self-organization for the condensate? Which of its features are universal? What happens when the range of fluid-element interactions is below the energy injection scale? Recently, we have also started to explore condensates that have both 2d-like and 3d-like interactions.
Read more
- Svirsky, A, and Frishman A. “Out-of-equilibrium fluxes shape the self-organization of locally-interacting turbulence”. Phys. Rev. Lett. 134(20), 204001 (2025).
- Svirsky, A., Herbert, C. and Frishman, A. “Two-dimensional turbulence with local interactions: statistics of the condensate.” Phys. Rev. Lett., 131(22), 224003 (2023).
- Frishman, A. and Herbert C. “Turbulence Statistics in a Two-Dimensional Vortex Condensate.” Phys. Rev. Lett. 120.20: 204505 (2018).
- Frishman A. “The culmination of an inverse cascade: mean flow and fluctuations.” Physics of Fluids 29.12: 125102. (2017).
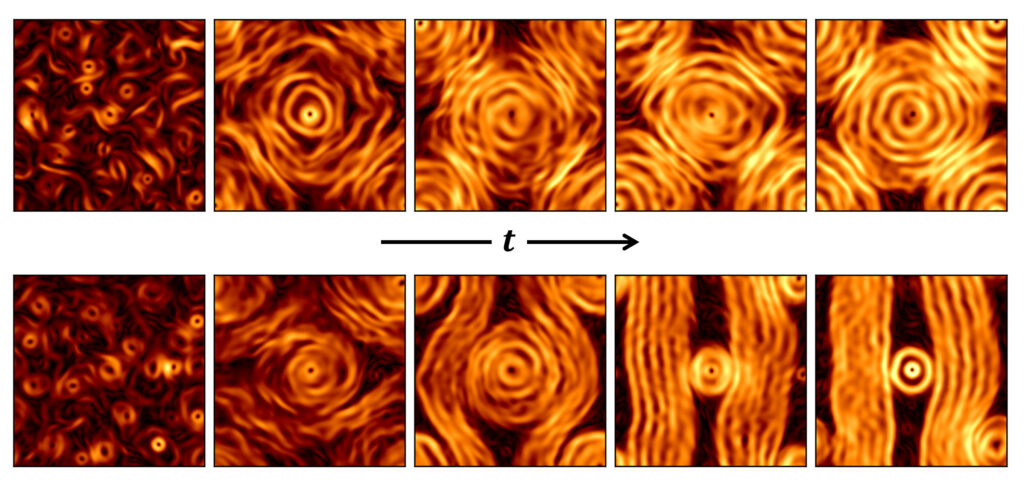
Subcritical transition to turbulence
Fluid flow generically becomes turbulent when the Reynolds number, which is the relevant control parameter, is sufficiently increased. In flows where the base state is linearly stable, termed subcritical flows, this transition occurs directly to a turbulent state, with turbulence appearing intermittently in space and time. With increasing Reynolds number, the system transitions between several different phases until finally reaching the homogeneous turbulent state.
Building on recent progress in the field, our work aims to understand the different possible phases and under which conditions they occur; the role of fluctuations and the mechanisms leading to transitions between phases and the generallity of the subcritical transition scenario.
Read more
- Svirsky, A., Grafke T. and Frishman A. “Self-Replication of Turbulent Puffs: On the edge between chaotic saddles”, arXiv:2505.05075.
- Frishman, A. and Grafke T. “Mechanism for turbulence proliferation in subcritical flows.” Proceedings of the Royal Society A 478.2265: 20220218, (2022).
- Frishman, A. and Grafke, T. “Dynamical landscape of transitional pipe flow“, Phys, Rev. E 105.4: 045108 (2022).
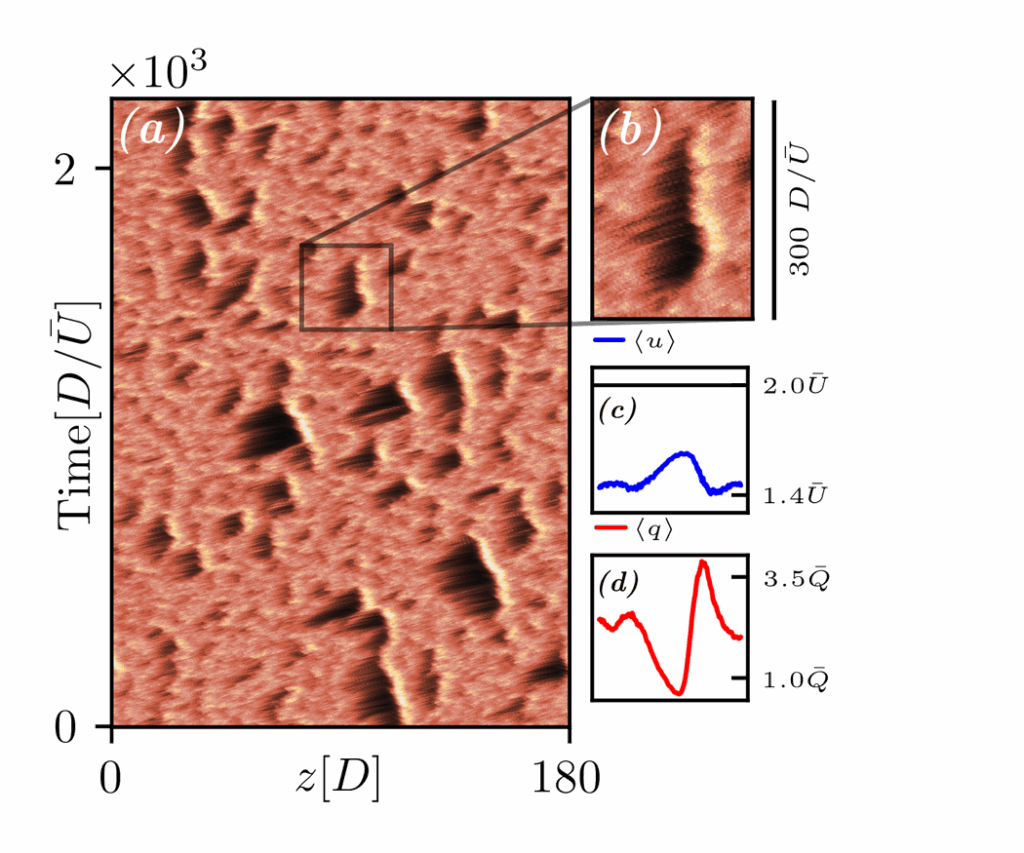
Clouds and their fate
Clouds consist of water droplets; as these droplets collide and coallese they grow, until eventually they start falling out of the cloud, producing rain. What fraction of the water in a cloud will remain in it after it rains down? How long will it live? The answer to these questions depends on the initial charatcrestics of the cloud. Our work aims to construct a minimal coarse-grained description of this depdnence, using ideal models of the droplet population dynamics in the cloud.
Read more
- Kapon, S., Jeevanjee N. and Frishman A. “Single-parameter effective dynamics of warm cloud precipitation.” arXiv:2409.05398
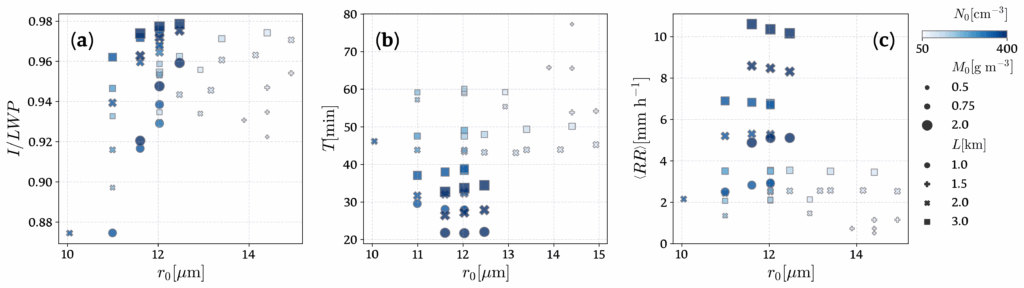
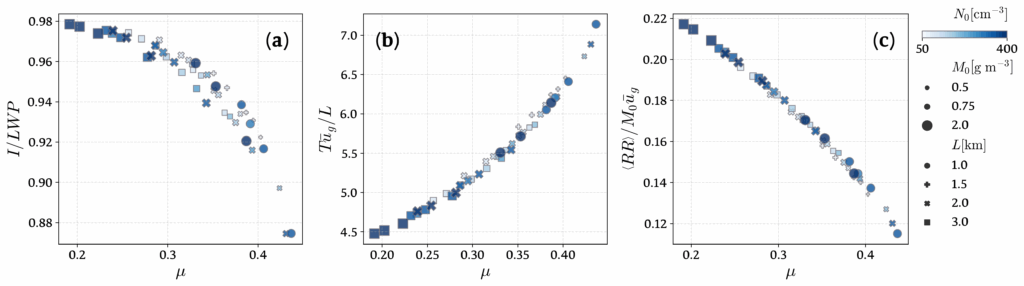
Cloud observables collapse when presented as a function of a dimensionless parameter quantifying accretion vs rainfall

Universality in the breakup of a fluid bridge
The breakup of a fluid object is a singular and dramatic process. We explore how a cylindrical soap film bridge breaks when stretched, and find that it always forms one large central satellite bubble. We show that the size of this bubble is extremely reproducible, and grows with the stretching rate and with the initial bridge aspect ratio. We trace the robustness of the size to an underlying universal dynamical solution.
Read more
- Frishman A. and Lecoanet, D. “Universality of satellites in the breakup of a stretched fluid bridge”, Phys. Rev. Fluids 10.6 (2025): 063604 (2025).
Stochastic force inference
Particles in biological and soft matter systems undergo Brownian dynamics: their deterministic motion, induced by forces, competes with random diffusion due to thermal noise. More broadly, Brownian dynamics is a generic and simple model for dynamical systems with noise.
Given only the noisy trajectories resulting from such dynamics – could we determine the equations that generated them? How would we do that in practice? Of particular interest are trajectories generated by an out-of-equilibrium process, in which case one would like to be able to identify the signatures of irreversibility and quantify it.
Our proposed solutions, including a practical inference method, are based on ideas from information theory and stochastic thermodynamics.
Read more
- Frishman, A. and Ronceray P. “Learning force fields from stochastic trajectories.” Phys. Rev. X 10.2: 021009 (2020).
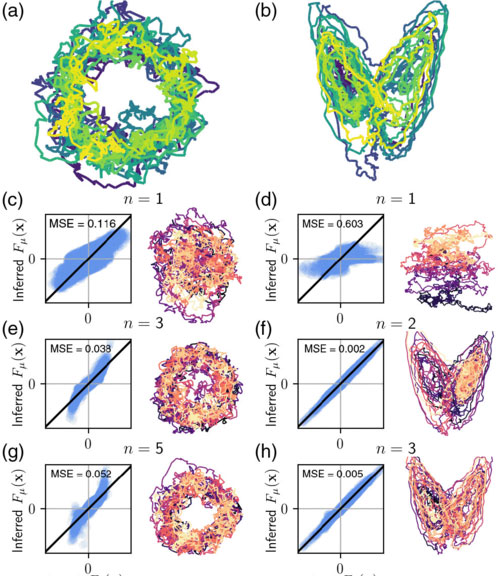
Figure from Frishman, A. and Ronceray P. Phys. Rev. X 10, 021009 (2020).
Lagrangian time irreversibility of turbulence
Turbulence is an out-of-equilibrium phenomena as evidenced by the flux of energy through scales. But how could you see that irreversibility if you are only watching particles in the flow? What is the manifestation of the energy flux, which is a property of the velocity field, for particles? What changes if the flow is compressible?
Read more
- Grafke, T., Frishman A., and Falkovich G. “Time irreversibility of the statistics of a single particle in compressible turbulence.” Phys. Rev. E 91.4, 043022, (2015).
- Frishman A. and Falkovich G. “A new type of anomaly in turbulence“. Phys. Rev. Lett.113.02, 024501, (2014).
- Falkovich, G., and Frishman A. “Single Flow Snapshot Reveals the Future and the Past of Pairs of Particles in Turbulence.” Phys. Rev. Lett.110.21 214502 (2013).
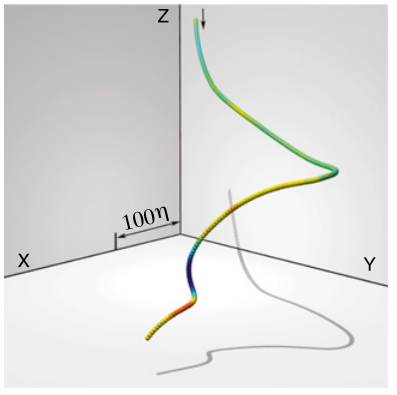
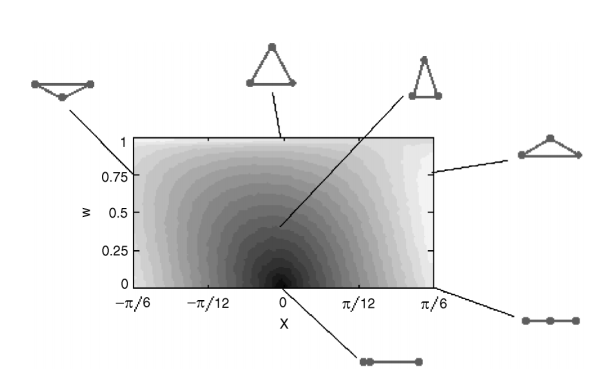
Lagrangian conservation laws
Conservation laws and symmetries play a central role in physics. Relatively recently, it was discovered that Lagrangian statistical conservation laws, related to the dynamics of particles, play a crucial role in the field theoretic description of turbulence. Their influence was demonstrated for the statistics of a field advected by the flow, and their form could be computed in simplified models for the velocity field. It remains unclear how to obtain such laws for a real turbulent velocity field, and what their influence could be on the field’s statistics. We have made some attempts in that direction.
Read more
- Falkovich, G., and Frishman A. “Single Flow Snapshot Reveals the Future and the Past of Pairs of Particles in Turbulence.” Phys. Rev. Lett.110.21 214502 (2013).
- Frishman, A., Boffetta, G., De Lillo, F., & Liberzon, A. “Statistical conservation law in two-and three-dimensional turbulent flows.” Phys. Rev. E 91.3, 033018, (2015).
· Banner Image Credit: NASA/Ocean Biology Processing Group, NASA Goddard Space Flight Center ·

