An important aspect of quantum many-body systems, which distinguishes them from classical ones, and allows for their unique character and behavior, is the quantum entanglement. Hence, to understand these systems we need to understand their entanglement structure. Furthermore, in numerical simulations of many-body systems, quantum entanglement is often the limiting factor. In particular, tensor network methods(such as DMRG), which are among the leading numerical techniques for many-body quantum systems, are based on low entanglement approximations of the many-body state. Understanding the structure and dynamics of entanglement can thus allow for more efficient simulations.
Operator dynamics in systems with local structure
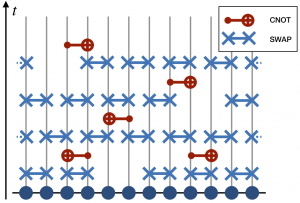 The growth of operator complexity in quantum systems is often characterized by the out-of-time-ordered correlator (OTOC), a quantity closely related to quantum chaos. The early time behavior of the OTOC in systems with large local Hilbert space dimension is known to exhibit a regime of exponential growth with an exponent known as the Lyapunov exponent. On the other hand, the existence of a well-defined Lyapunov regime in generic quantum many-body systems is still debated. We have proposed a criterion for the presence of a prolonged regime of exponential growth, and thus for the existence of a well-defined Lyapunov exponent in systems with spatial structure and local interactions, demonstrating it on a minimally structured model for chaotic quantum dynamics – a unitary random circuit with tunable interactions.
The growth of operator complexity in quantum systems is often characterized by the out-of-time-ordered correlator (OTOC), a quantity closely related to quantum chaos. The early time behavior of the OTOC in systems with large local Hilbert space dimension is known to exhibit a regime of exponential growth with an exponent known as the Lyapunov exponent. On the other hand, the existence of a well-defined Lyapunov regime in generic quantum many-body systems is still debated. We have proposed a criterion for the presence of a prolonged regime of exponential growth, and thus for the existence of a well-defined Lyapunov exponent in systems with spatial structure and local interactions, demonstrating it on a minimally structured model for chaotic quantum dynamics – a unitary random circuit with tunable interactions.
