In most magnetic materials interactions between localized magnetic moments, or spins, give rise to some form of magnetic ordering as the system is cooled down close to zero temperature. However, in some cases, competing interactions are present, resulting in frustration which can prevent the system from ordering. Evading the paradigm of spontaneous symmetry breaking and thus a description in terms of a mean-field, these systems realize novel phases of matter termed spin liquids. I am interested in the characterization and identification of these states of matter in theoretical models, as well as in finding clear signature for the realization of these phases in experiments.
Novel phases of matter in systems with spin and orbital degeneracies
In a few recent studies, my collaborators and I have explored the nature of the ground state when the electrons possess an additional pseudo-spin degree of freedom. Such a situation can arise in materials with orbital degeneracy, as well as in moiré superlattices with valley degeneracy. Different combinations of the electronic spin and orbit give rise to four flavors of fermions that are present in the system. Therefore, a natural route to exploring the phase diagram of such systems is starting from SU(4)-symmetric models. When the electron density in the system corresponds to an integer number of electrons per lattice site, and the on-site repulsive interactions are strong, the system is driven into the Mott-insulating phase and can be described by an antiferromagnetic Heisenberg model. Focusing on the case of a triangular lattice, we studied both the case of half-filling (two electrons per site) and quarter-filling (single electron per site).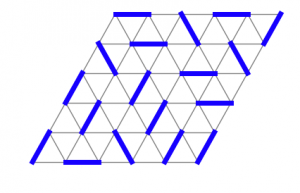
In the case of half-filling we found that the low energy properties of the model can be captured by an effective dimer model. Investigating the resulting dimer model numerically using exact diagonalization, we found that the ground state breaks translation invariance, forming a valence bond solid (VBS) with a 12-site unit cell. 
In the case of quarter-filling, carrying out a numerical DMRG study, we found striking evidence for a gapless liquid with an emergent Fermi surface of neutral quasi-particles in the ground state of the system. This state bears a resemblance to a metal when (thermal) transport or thermodynamic properties, such as magnetic susceptibility or specific heat, are considered, even though the charges in the system are immobile. This result is particularly surprising, as known realizations of such gapless phases in systems of SU(2) spins usually require very complicated Hamiltonians. In the SU(4) case, we find that the Fermi surface state can be realized in a very simple model with just nearest-neighbor Heisenberg interactions.
Read more:
- Anna Keselman, Lucile Savary, and Leon Balents, Dimer description of the SU(4) antiferromagnet on the triangular lattice, SciPost Phys., 8:76, 2020
- Anna Keselman, Bela Bauer, Cenke Xu, and Chao-Ming Jian, Emergent fermi surface in a triangular-lattice SU(4) quantum antiferromagnet, Phys. Rev. Lett., 125:117202, Sep 2020
Dynamical response of low-dimensional spin systems
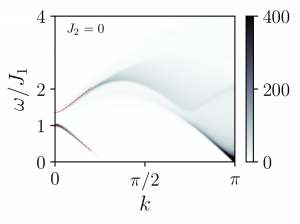While the ground state of the system determines the nature of the low energy excitations, dynamical probes give access to the spectrum of the system at all energy scales. Furthermore, studies of response functions that can be probed experimentally, e.g. the dynamical spin susceptibility that is obtained in inelastic neutron scattering, allow for direct comparison between theory and experiments. In low-dimensional systems such response functions can be simulated numerically with high efficiency and accuracy using matrix product state (MPS) based techniques.
In a recent study, we have analyzed the dynamical structure factor of a spin-1/2 antiferromagnetic chain in the presence of an external magnetic field, uncovering signatures of quasi-particle interactions in this simple and paradigmatic model known to host fractionalized spinon excitations.
Read more:
- Anna Keselman, Leon Balents, and Oleg A. Starykh, Dynamical signatures of quasi-particle interactions in quantum spin chains, Phys. Rev. Lett., 125:187201, Oct 2020