Spin Glasses

Our major finding is:

Mapping exotic spin correlations by field dependent muon spin-lattice relaxation measurements.

Traditionally, the spin lattice relaxation time of a muon in a magnetic environment, also known as T₁, is interpreted using the concept of spin correlation time. However, in some situations, no correlation time could be assigned to the spins, and a different interpretation of T₁ is required. Our group recently developed such an interpretation. As a test case spin glasses where chosen since the theoretical expectation is for a time scale invariant spin evolution over a few decades. Indeed, the experiments show that the spin correlation function is best described by a product of a power law and a cut-off functions and that the slowing down spin fluctuations are manifested essentially by the temperature dependence of the power law term.
In a muon field dependent T₁ measurements, one determines the time t it takes the polarization P(H,t) of a muon to reach thermal equilibrium with the system under investigation, from an initial non-equilibrium polarization. The magnetic field H is applied along the initial muon spin direction. The muon flip rate (1/T₁) depends on how popular is the Larmor frequency (w_L=g_mH) among the lattice fluctuations, since in order for the muon to flip from up to down states it must absorb, or release, the energy hw_L to the lattice (depending on the field direction). In other words, T₁ will be short if the Fourier transform of the spin-spin correlation function q(t)=<S(t)S(0)> atw_L is large, and vice versa.

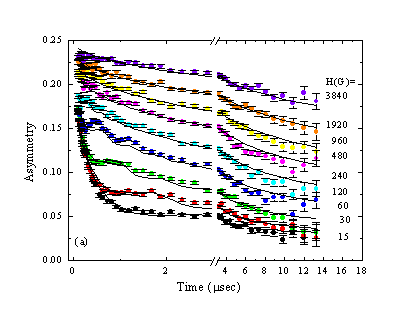
Figure 1 Asymmetry versus time in the spin glass AgMn(0.5 @ %) at T>T_g for various longitudinal magnetic fields. The solid lines are fit to a model relating T₁ to a correlation function, and a cutoff power law function (as in Eq. 1) is used.

It is customary to assume that the correlation function decays exponentially with some correlation time t and therefore the Fourier transform of q(t) is a Lorentzian in terms of the field H. Thus, at asymptotically high fields we expect T₁ proportional to H², and the muon polarization P(H,t) should be a function of the ratio t/H². This conclusion holds even if instead of having a single correlation time in the system there is a distribution of t’s. However, the assumption that there is a correlation time could be incorrect to start with, and in many complex systems q(t) can be strongly non-exponential, with time scale invariance or hierarchical relaxation. Here we demonstrate the presence of non-exponential correlation functions in nature by performing mSR measurements on the Heisenberg spin glass AgMn(0.5 at. %). We chose this system since numerical work on glasses indicates the presence of “exotic” correlation functions. We also show how to determine the functional form of q(t) using the field dependent muon depolarization measurements.

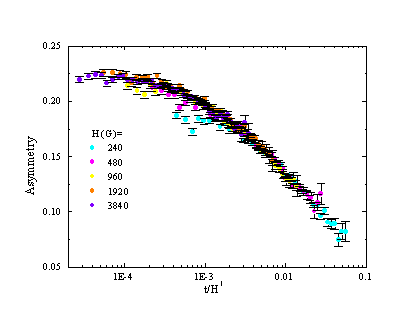
Figure 2 The asymmetry from Fig. 1 plotted as a function of t/H for fields higher than 240 G. The fact that the asymmetry is a function oft/H and not t/H² rules out the possibility of describing the spin correlation function with one or many correlation times.

Figure 1 shows representative data sets of the muon asymmetry A(H,t), which is proportional to P(H,t), at T=2.9 K (above T_g=2.8K) and at various fields. Note the break in the time axis. Clearly, H affects the muon polarization very strongly over more than two orders of magnitude in magnetic field. In order to test whether a single or a distribution of correlation time could describe this system we normalize the time t by the field to some power. We found that for high fields, the muon polarization is a function of t/H and not t/H². This is demonstrated in Fig. 2. Thus, an exponential relaxation function or even a sum of exponential relaxations cannot account for this data. One must search for a correlation function whose Fourier transform falls off like 1/w at high frequencies. This requirement determines the behavior of the correlation function at early times.

For low values of H, in Fig. 1 clear wiggles are observed in the beginning of the data. The source of the wiggles are those muons for which a local transverse magnetic field B_T , has not relaxed abruptly during the time of one rotation. These muons will oscillate around the vector sum of both internal and external fields at a frequency w=g_m(H²+B_T²)^1/2. Since at T>T_g there is a distribution of B_T with zero average, the contribution of the local internal fields will show up as a relaxation of the wiggles, while the frequency of the wiggles will be at w_L. However, if there is a cutoff time t, then by the time t>t abrupt field relaxation occurs for all muons. Therefore, wiggle pattern will not be seen for longer times. As a result, the observation of a “wiggle” pattern up to time t is the proof that there are local fields that do not relax abruptly within time t. Thus the observation of wiggles gives us a model independent estimate of t. 

The combination of the asymptotic field dependence shown in Fig. 2 and the wiggles observed in Fig. 1 forces us to consider a cut off power law correlation function of the form

1) 

where x is a dynamical power. This, in fact, is the function used to analyze most of the molecular dynamic numerical work on spin glasses. In our paper we demonstrate how this function is introduced into the general theory of spin-lattice relaxation. The fits shown in Fig. 1 are obtained using this theory and Eq. 1. The fits capture the long time behavior very well and the frequency of the wiggles. However, the account for the relaxation of the wiggles is not perfect. 

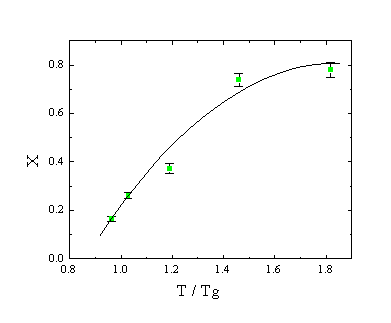
We have performed these measurements at different temperatures above Tg. At each temperature data was collected at 9 different fields and the value of x was determined. In Fig. 3 we depict x(T). As the temperature decreases x decreases. In fact, our analysis show that x is the only temperature dependent parameter. Therefore, stretching out the power law part and making x small manifests the slowing down of spin fluctuation upon cooling.

Figure 3 The dynamic power x (from Eq. 1) plotted versus temperature. The slowing down of spin fluctuations is manifested in the decrease of x upon cooling.

The Israeli Academy of Science funded this research project. The project name is Muon spin relaxation in spin glasses, and its duration was 1997-2000. The principal investigator is Amit Keren.

We have published the following papers on the subject: