.[latexpage]
Read more in our publication:
- Ness, G., Shkedrov, C., Florshaim, Y., Sagi., Y. Realistic Shortcuts to Adiabaticity in Optical Transfer, New J. Phys. 20, 095002 (2018).
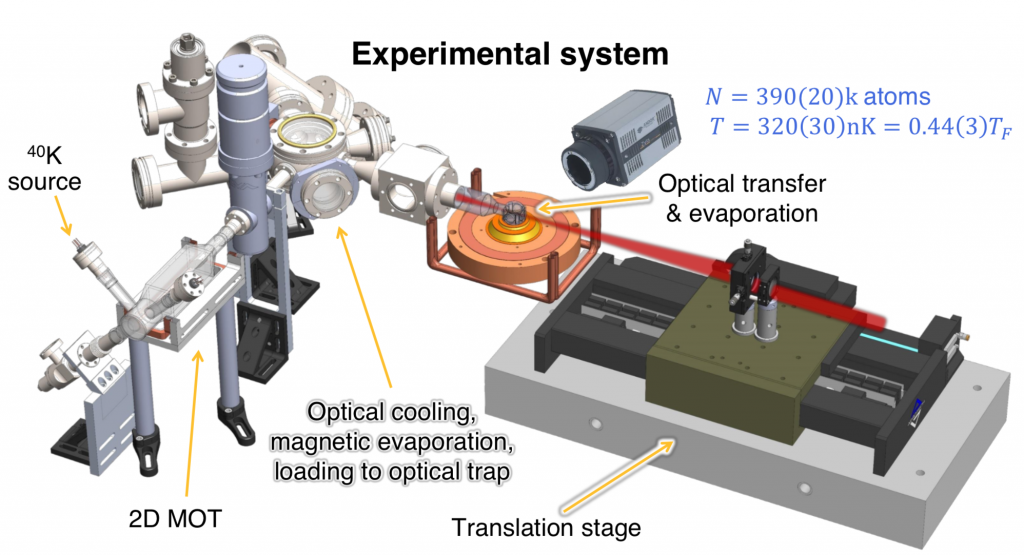
The question we ask is how to perform dynamical changes as fast as possible without causing heating? the prime example we focus on is optical transport of ultracold atoms between two locations.
Why non-adiabatic transport? True adiabaticity takes asymptotically long time which leads to decoherence, noise and overall slower repetition rate.
The solution: Shortcuts to Adiabaticity (STA).
Shortcuts to adiabaticity refers to a class of schemes enabling the fast variation of a system Hamiltonian while still reaching a specific target state. They derived by cleverly tailoring the fast driving protocol such that the system attains the desired final state without being adiabatic. However, the experimental implementation of STA for rapid atoms transfer suffers from an inherent problem arising from the fact that these driving profiles are suited for the atoms trajectory as in practice the trap coordinate is the controlled one. In our research, the experimental realization of these STA schemes was achieved for optical transfer of ultracold fermionic atoms. We found that in order to lift conflicting boundary conditions it is necessary to increase the number of degrees of freedom in the trajectory, develop and demonstrate two complementary methods to achieve this; the first acts as a “correction” to the original trajectory, while in the second approach the trajectory is redesigned to account for all boundary conditions. Using both methods, we demonstrate successful transports of cold atoms in the highly non-adiabatic regime.
Method 1: Spectral correction
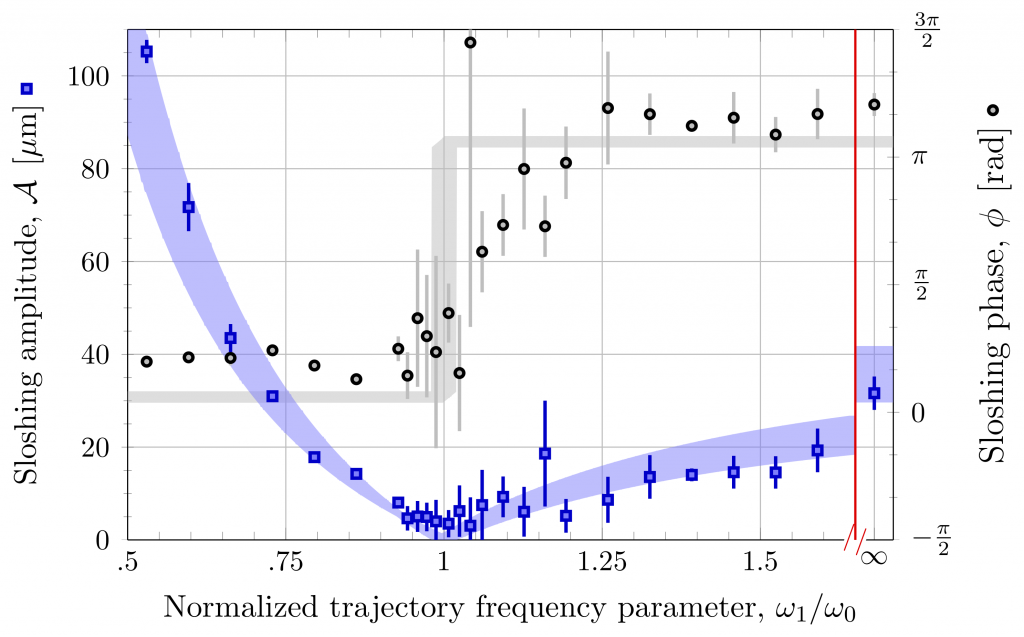
Approximating the optical potential to a harmonic one, the requirement for STA transport reduces to zero sloshing amplitude at transport end. The terminate sloshing amplitude can be analytically calculated by the trapping frequency Fourier component of the trap velocity trajectory,
$\mathcal{A}\left(t_{f}\right)
=\left|\intop_{0}^{t_{f}}\exp\left(-i\omega_{0}t\right)\dot{z}_{\cup}\left(t\right)\mathrm{d}t\right|$.
The idea in this method is to introduce a new spectral component to an existing trajectory which can be implemented experimentally such that it will satisfy all required boundary conditions and the sloshing amplitude will vanish. We can cancel the sloshing amplitude by adding a new spectral component at the trapping frequency such that their sum is zero. A scan of the correction amplitude at the optimal correction phase is presented in Fig.1
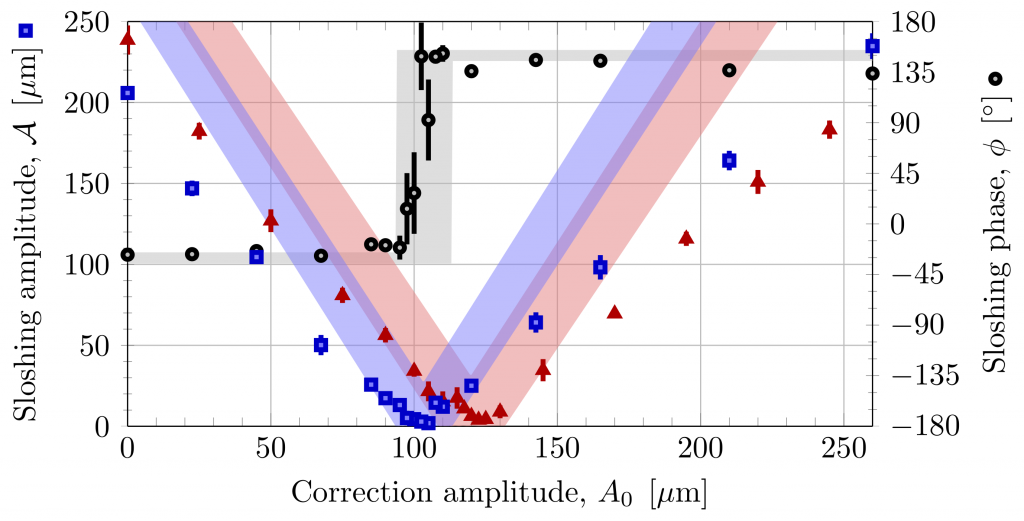
Method 2: Spectral correction