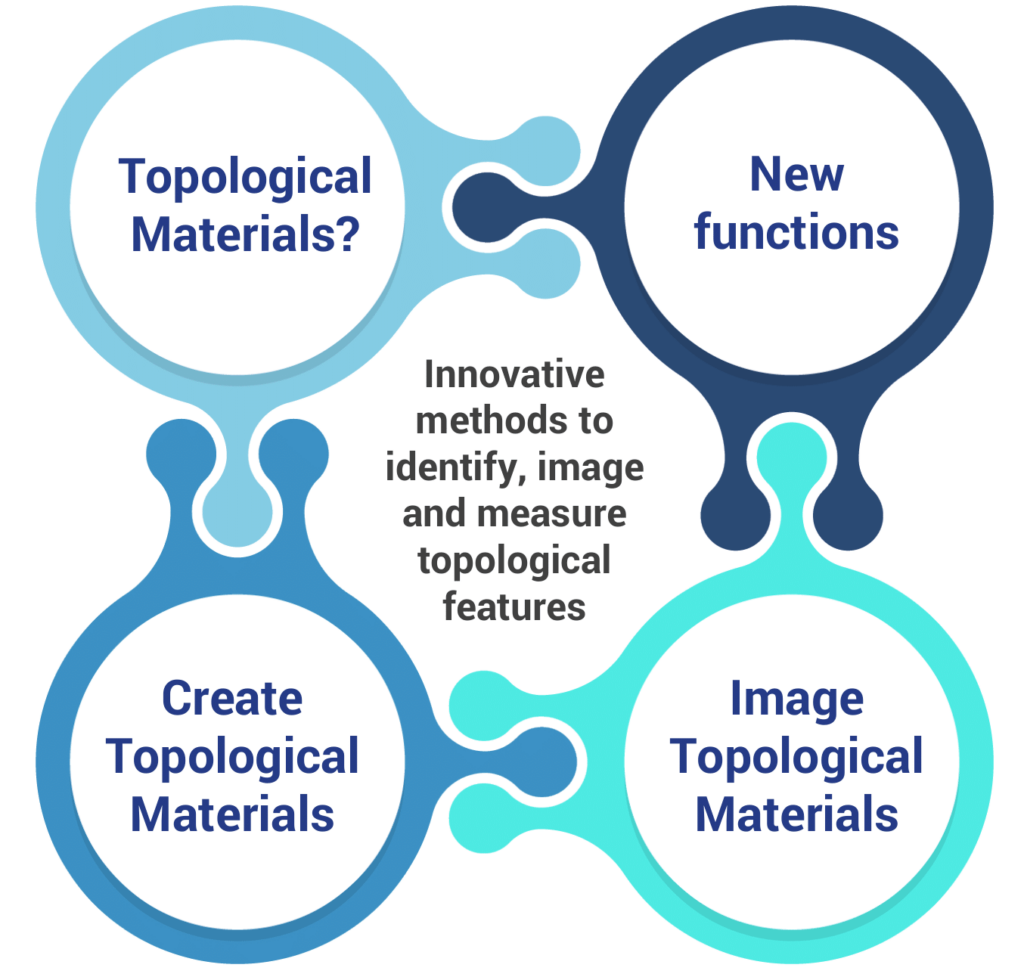
Welcome
Condensed matter sits at the crossroad between several fields of physics, such as quantum physics, equilibrium and out of equilibrium physics, quantum field theory, cold atomic gases and mesoscopic physics, among others.
In our group, we enjoy standing at those crossroads and to use these overlaps as efficiently as possible. To know more, go to the entries below or, even better, come to join forces.



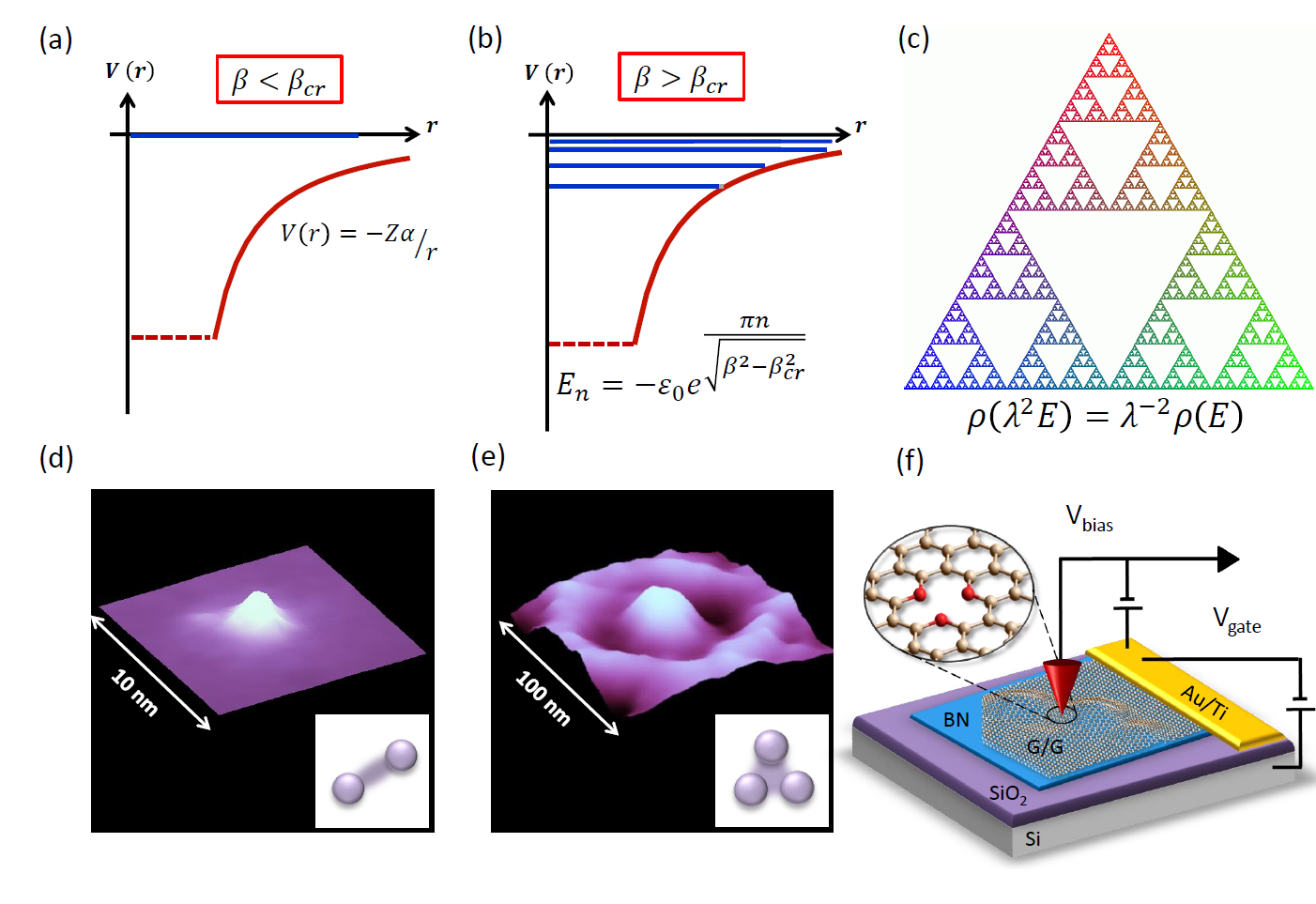 Scale invariance is a property of our everyday environment. Its breaking gives rise to less common but beautiful structures like fractals.
Scale invariance is a property of our everyday environment. Its breaking gives rise to less common but beautiful structures like fractals. 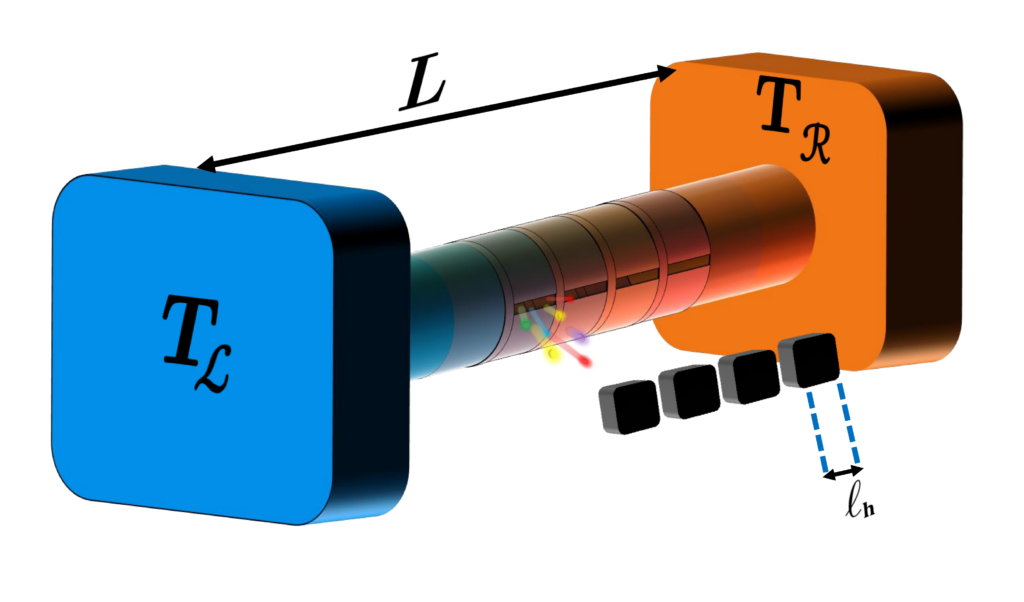 The best understood systems in statistical mechanics are those at equilibrium (fixed energy) or in thermal contact with a thermostat. These systems are well descri-
The best understood systems in statistical mechanics are those at equilibrium (fixed energy) or in thermal contact with a thermostat. These systems are well descri-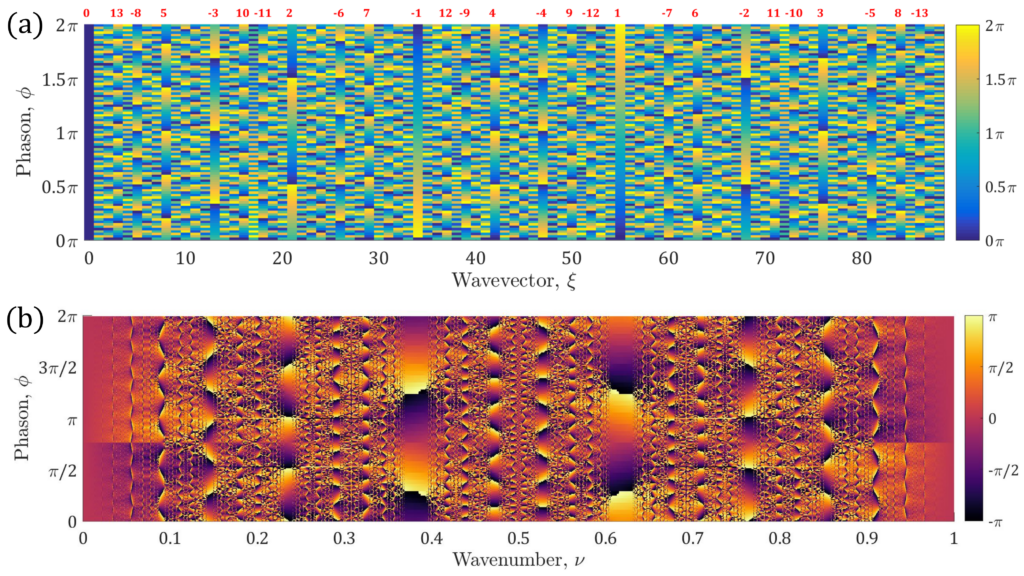

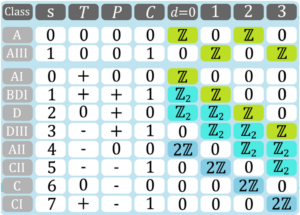
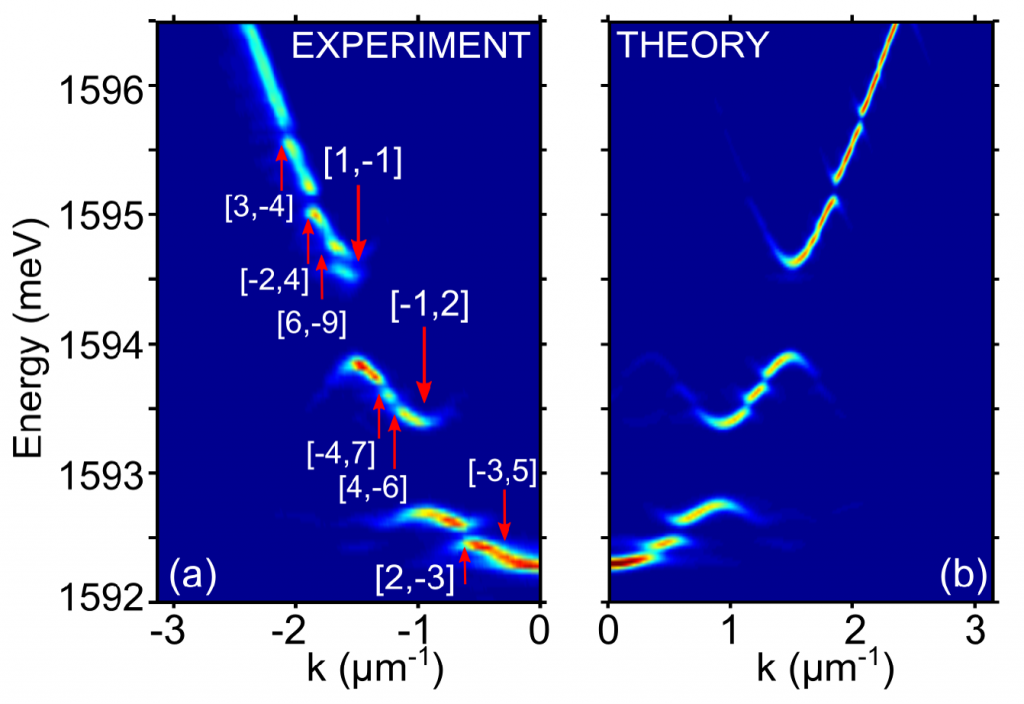 Fractals define a new realm to study basic phenomena in quantum field theory and statistical mechanics. This results from speci-
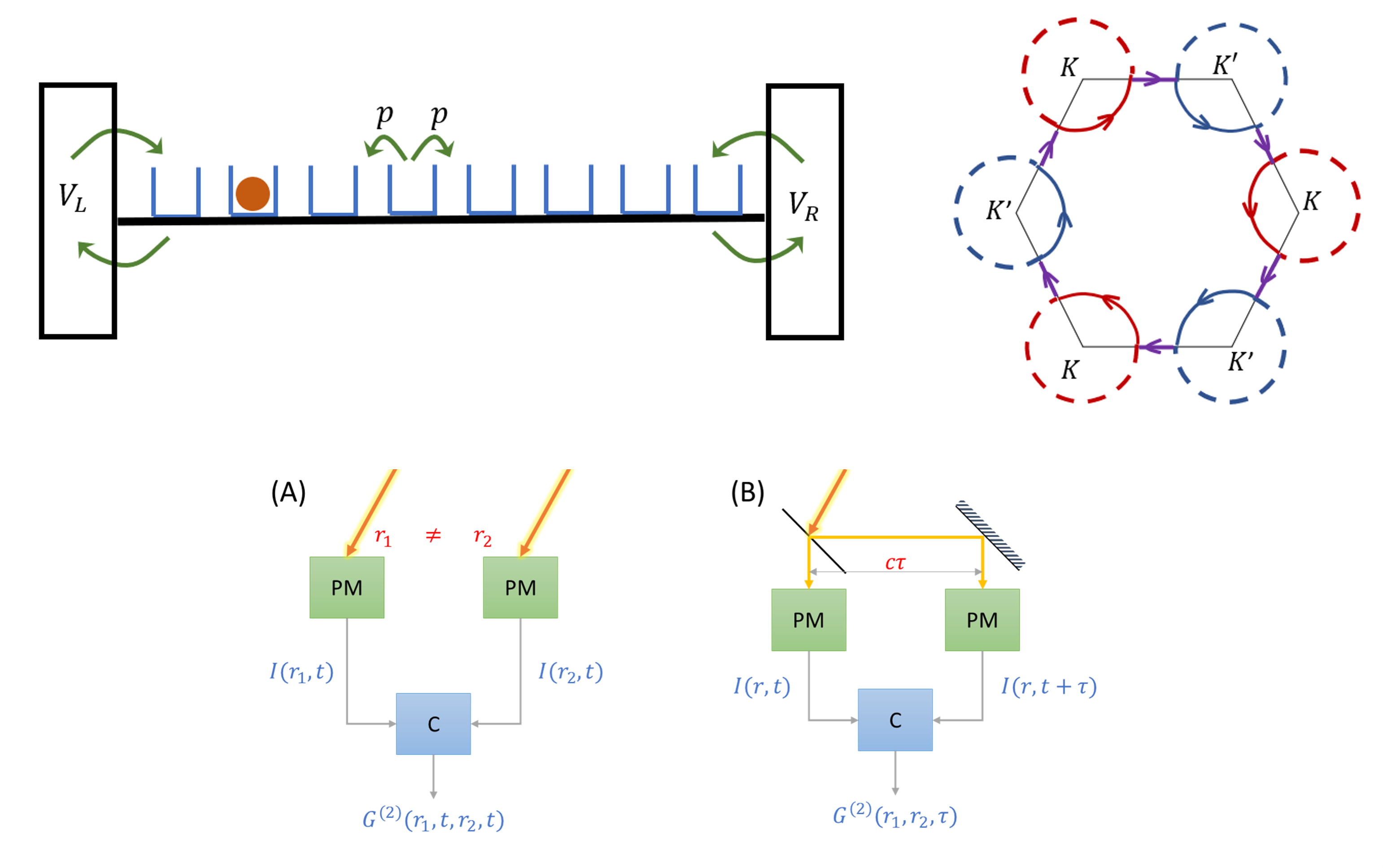
Fractals define a new realm to study basic phenomena in quantum field theory and statistical mechanics. This results from speci-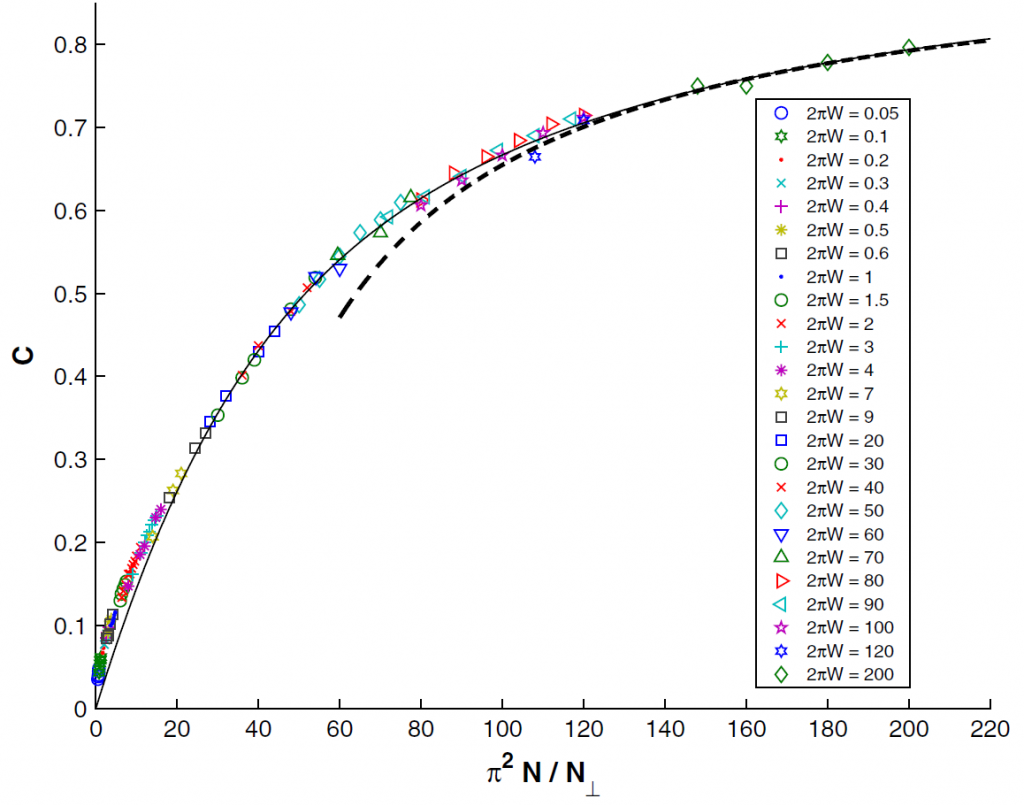 Spontaneous emission of an atom coupled to quantum vacuum fluctuations is well understood. When two or more atoms are bro-
Spontaneous emission of an atom coupled to quantum vacuum fluctuations is well understood. When two or more atoms are bro-